NCERT/CBSE
- CBSE Class 10 Syllabus
- NCERT Class 10 Solutions

https://www.urbanpro.com/ncert-solutions/class-10/maths-pair-linear-equations-two-variable-exercise-3-6

Learn Exercise 3.6 with Free Lessons & Tips

Download Solutions as PDF

Question 1:

Solve the following pairs of equations by reducing them to a pair of linear equations:

$(i) \frac{1}{2x}+\frac{1}{3y}=2, \frac{1}{3x}+\frac{1}{2y}=\frac{13}{6}$

$(ii) \frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2, \frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1$

$(iii) \frac{4}{x}+3y=14, \frac{3}{x}-4y=23$

$(iv) \frac{5}{x-1}+\frac{1}{y-2}=2, \frac{6}{x-1}-\frac{3}{y-2}=1$

$(v) \frac{7x-2y}{xy}=5, \frac{8x+7y}{xy}=15$

$(vi) 6x+3y=6xy, 2x+4y=5xy$

$(vii) \frac{10}{x+y}+\frac{2}{x-y}=4, \frac{15}{x+y}-\frac{5}{x-y}=-2$

$(viii) \frac{1}{3x+y}+\frac{1}{3x-y}=\frac{3}{4}, \frac{1}{2(3x+y)}-\frac{1}{2(3x-y)}=\frac{-1}{8}$

Solution 1:

$(I) Let \frac{1}{x}=p and \frac{1}{y}= q$

According to the question, The equation reduces to

$\frac{p}{2}+\frac{q}{3}=2$ ,

$\Rightarrow 3p+2q-12=0.................(i)$

$\frac{p}{3}+\frac{q}{3}=\frac{13}{6}$

$\Rightarrow 2p+3q-13=0...............(ii)$

Using cross-multiplication method, we get:

$\frac{p}{-26-(-36)}=\frac{q}{-24-(-39)}=\frac{1}{9-4}$

On solving we get $p=2, q=3$

Hence, $x=\frac{1}{2}, y=\frac{1}{3}$

$(ii) let \frac{1}{\sqrt{x}}=p$ and $\frac{1}{\sqrt{y}}=q$

From the question, the equation reduces to

$2p+3q=2............(i)$

$4p-9q=-1.............(ii)$

Multiplying equation (1) by 3, we get :
6p + 9q = 6 (3)
Adding equation (2) and (3), we get: $p=\frac{1}{2} , q=\frac{1}{3}$

$\frac{1}{\sqrt{x}}=\frac{1}{2}$ ,

$\sqrt{x}=2, x=4$

$\frac{1}{\sqrt{y}}=\frac{1}{3}$

$\sqrt{y}=3, y=9$

Hence, $x=4, y=9$

$(iii) let \frac{1}{x}=p$

From the question, the given equation reduces to

$4p+3y=14$ $.............(i)$

$3p-4y=23.............(ii)$

Using cross multiplication, we get,

$\frac{p}{-69-56}=\frac{y}{-42-(-92)}=\frac{1}{-16-9}$

$p=5, y=-2$

$p=\frac{1}{x}=5, x=\frac{1}{2}$

Hence, $x=\frac{1}{5} , y= -2$

$(iv) Let \frac{1}{x-1}=p, \frac{1}{y-2}=q$

The equation reduces to

$5p+q=2...............(i)$

$6p-3q=1..............(ii)$

on multiplying the two equations, we get,

$15p+3q=6...............(iii)$

Adding (ii) and (iii), we get $p=\frac{1}{3}$

Putting the value of p in (i) $q=\frac{1}{3}$

$p=\frac{1}{x-1}=\frac{1}{3}, q=\frac{1}{y-2}=\frac{1}{3}$

Hence, $x=4 , y= 5$

$(v)$

$\frac{7}{y}-\frac{2}{x}==5..............(i)$

$\frac{8}{y}+\frac{7}{x}=15..........(ii)$

$Let \frac{1}{x}=p and \frac{1}{y}= q$

The equation reduces to

$-2p+7q-5=0.................(iii)$

$7p+8q-15=0 ................(iv)$

Using cross multiplication, we get

$\frac{p}{-105-(-40)}=\frac{q}{-35-30}=\frac{1}{-16-49}$

On solving, $p=1, q=1$

$p=\frac{1}{x}=1, q= \frac{1}{y}= 1$

Hence, $x=1, y=1$

$(vi) \frac{6}{y}+\frac{3}{x}=6..............(i)$

$\frac{2}{y}+\frac{4}{x}= 5............(ii)$

$Let \frac{1}{x}=p and \frac{1}{y}= q$

The equation reduces to

$3p+6q-6=0$

$4p+2q-5=0$

By cross multiplication, we get

$\frac{p}{-3-(-12)}=\frac{q}{-24-(-15)}=\frac{1}{6-24}$

On solving, $p=1, q=\frac{1}{2}$

Therefore, $x=1, y=2$

$(vii) Let \frac{1}{x+y}=p, \frac{1}{x-y}=q$

The equation reduces to

$10p+2q-4=0............(i)$

$15p-5q+2=0............(ii)$

Using cross multiplication,

$\frac{p}{4-20}=\frac{q}{-60-20}=\frac{1}{-50-30}$

On solving we get $p=\frac{1}{5} , q= 1$

$x+y=5........(iii)$

$x-y=1..............(ii)$

Adding (iii) and (iv) $x=3, y=2$

$(viii) Let \frac{1}{3x+y}=p, \frac{1}{3x-y}=q$

$P+q=\frac{3}{4}...............(i)$

$p-q= \frac{-1}{4}$ $..............(ii)$

Adding (i) and (ii) we get $p=\frac{1}{4} , q=\frac{1}{2}$

$p= \frac{1}{3x+y}=\frac{1}{4},q= \frac{1}{3x-y}=\frac{1}{2}$

$3x+y=4........(iii)$

$3x-y=2............(iv)$

Adding the above equations, we get x=1, y=1

Comments

Tasneem

Question 2:

. Formulate the following problems as a pair of equations, and hence find their solutions:

(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.

(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.

(iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately

Solution 2:

(i) Let the speed of Ritu in still water and the speed of stream be x km/h and y km/h respectively.

Speed of Ritu while rowing upstream = (x-y) km/h

Speed of Ritu while rowing downstream = (x + y) km /h

$2(x+y)= 20$

$x+y=10.............(i)$

$2(x-y)=4$

$x-y=2..........(ii)$

Adding equations (1) and (2), we obtain:

2x = 12

x = 6

Putting the value of x in equation (1), we obtain:

y = 4

Thus, Ritu’s speed in still water is 6 km/h and the speed of the current is 4 km/h.

(ii) Let the number of days taken by a woman and a man to finish the work be x and y respectively.

Work done by a woman in 1 day =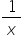

Work done by a man in 1 day =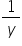

$\frac{2}{x}+\frac{5}{y}= \frac{1}{4}.............(i)$

$\frac{3}{x}+\frac{6}{y}= 1........(ii)$

$Let p= \frac{1}{x}, q= \frac{1}{y}$

The equation reduces to

$8p+20q=1$

$9p+18q=1$

Using cross multiplication,

$\frac{p}{-20-(-18)}=\frac{q}{-9-(-8)}=\frac{1}{144-180}$

On solving, $p=\frac{1}{18}, q=\frac{1}{36}$ so $x=18, y=36$

The number of days taken by the a woman is 18 and that taken by a man is 36.

(iii) Let the speed of train and bus be u km/h and v km/h respectively.

$Time= \frac{distance}{speed}$

$\frac{60}{u}+\frac{240}{v}=4.......(i)$

$\frac{100}{u}+\frac{200}{v}=\frac{25}{6}............(ii)$

$let p=\frac{1}{u}, q=\frac{1}{v}$

The equation reduces to $60p+240q=4...........(iii)$

$600p+2400q=25..........(v)$

On subtracting (iv) from (v) we get

$q=\frac{1}{80 }, p=\frac{1}{60}$

Thus the train travels at a speed of 60km/hr and the speed of the bus is 80km/hr.

Comments

Tasneem

All Exercises - Chapter 3 - Pair of Linear Equations in Two Variable

Exercise 3.1

Exercise 3.2

Exercise 3.3

Exercise 3.4

Exercise 3.5

Exercise 3.6

Exercise 3.7

Feedback:

How helpful was it?

This article changed my life! This article was informative. I have a question.

How can we Improve it?

This article contains incorrect information. This article doesn't have the information I am looking for. I have a question.

Please tell us how it changed your life ^*

Please enter your feedback

Please enter your question below and we will send it to our tutor communities to answer it ^*

Please enter your question

Please select your tags

Please select a tag

Name ^*

Enter a valid name.

Email ^*

Enter a valid email.

Email or Mobile Number: ^*

Please enter your email or mobile number

Sorry, this phone number is not verified, Please login with your email Id.

Password: ^*

Please enter your password

By Signing Up, you agree to our Terms of Use & Privacy Policy

Thanks for your feedback

About UrbanPro

UrbanPro.com helps you to connect with the best Class 10 Tuition in India. Post Your Requirement today and get connected.

I am a Student I am a Tutor
Name*	Please enter your full name. Please enter institute name.
Email*	Please enter your email address.
Phone*	Please enter a valid phone number.
Location*	Please enter a pincode or area name.
City*	Please enter city name.
Category*	Please enter category.
Gender*	Male Female Please select your gender.
Email ID/ Mobile No.*	Please enter either mobile no. or email.
Enter Password*	Please enter OTP Please enter Password Sorry, this phone number is not verified, Please login with your email Id.

Learn Exercise 3.6 with Free Lessons & Tips

All Exercises - Chapter 3 - Pair of Linear Equations in Two Variable

About UrbanPro

Looking for Class 10 Tuition Classes?

Looking for Class 10 Tuition Classes?