Equation of tangent at P(x,y) to the curve y=f(x) is given as
Y-y=dy/dx(X-x)
Equation of Normal at P(x,y) to the curve y=f(x) is given as
Y-y=-1/dy/dx(X-x)
By applying the condition of perpendicularity
If product of slopes of lines will be equal to -1 lines are perpendicular
as we know that normal and tangent will be perpendicular to each other
m1m2=-1
let slope of tangent is m1=dy/dx
so solpe of normal will be m2=-1/m1=-1/dy/dx
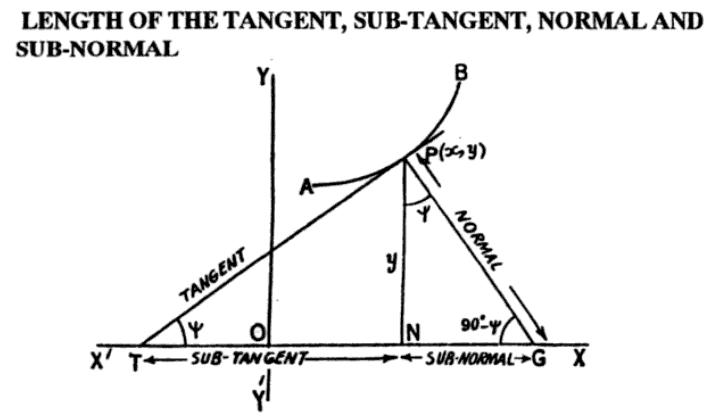
length of tangnet will be y=√1+(dx/dy)2
Length of normal will be y=√1+(dy/dx)2
length of Sub-Tangent will be ydx/dy
length of Sub-normal will be ydy/dx


 0
0

