Find the best tutors and institutes for Class 6 Tuition
Search in
What is the disadvantage in comparing line segments by mere observation?
By mere observation, we cannot be absolutely sure about the judgement. When we compare two line segments of almost same lengths, we cannot be sure about the line segment of greater length. Therefore, it is not an appropriate method to compare line segments having a slight difference between their lengths. This is the disadvantage in comparing line segments by mere observation.
Why is it better to use a divider than a ruler, while measuring the length of a line segment?
It is better to use a divider than a ruler because while using a ruler, positioning error may occur due to the incorrect positioning of the eye.
Draw any line segment, say
. Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB?
[Note: If A, B, C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B]
It is given that point C is lying somewhere in between A and B. Therefore, all these points are lying on the same line segment. Hence, for every situation in which point C is lying in between A and B, it may be said that AB = AC + CB.
For example,
is a line segment of 6 cm and C is a point between A and B, such that it is 2 cm away from point B. We can find that the measure of line segment 
comes to 4 cm.
Hence, relation AB = AC + CB is verified.
If A, B, C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two?
Given that,
AB = 5 cm
BC = 3 cm
AC = 8 cm
It can be observed that AC = AB + BC
Clearly, point B is lying between A and C.
Verify, whether D is the mid point of 
.
From the given figure, it can be observed that
= 4 − 1 = 3 units
= 7 − 4 = 3 units
= 7 − 1 = 6 units
Clearly, D is the mid-point of AG.
If B is the mid point of 
and C is the mid point of
, where A, B, C, D lie on a straight line, say why AB = CD?
Since B is the mid-point of AC,
AB = BC (1)
Since C is the mid-point of BD,
BC = CD (2)
From equation (1) and (2), we may find that
AB = CD
Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
This task must be performed by the students on their own. Randomly draw some triangles and measure their lengths.
For example, we have drawn a few for your reference.
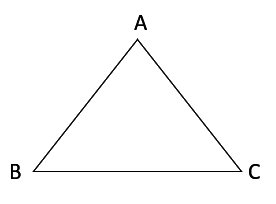
Here AB = 1 cm, BC = 1 m, AC = 1 cmsum of two sides> third side
Here AB = 4 cm,BC = 3 cm and AC = 5 cmsum of two sides> third side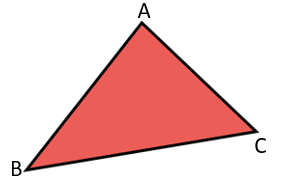
Here AB = 3 cm,BC = 3 cm and AC = 5 cmsum of two sides> third side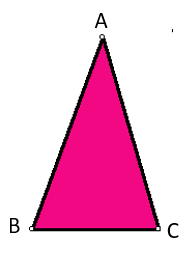
Here AB = 7 cm,BC = 7 cm and AC = 6 cmsum of two sides> third side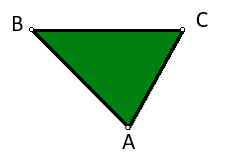
Here AB = 8 cm,BC = 9 cm and AC = 10 cmsum of two sides> third side
How helpful was it?
How can we Improve it?
Please tell us how it changed your life *
Please enter your feedback
UrbanPro.com helps you to connect with the best Class 6 Tuition in India. Post Your Requirement today and get connected.
Find best tutors for Class 6 Tuition Classes by posting a requirement.
Get started now, by booking a Free Demo Class
