Find the best tutors and institutes for Class 10 Tuition
Search in
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients: (i) (ii)
(iii)
(iv)
(v)
(vi)
Therefore, the zeroes are -2 and 4
Verification:
α= -2 β=4
α+β= -
-2+4=-(-2)
2=2
verified.
αβ= constant term/ coefficient of
, verified.
Therefore the zeroes are
Verification:
α= β=
α+β= -
1=1, verified
αβ= constant term/ coefficient of
verified
Therefore the zeroes are
Verification:
α= β=
α+β= -
Hence verified.
αβ= constant term/ coefficient of =
Therefore the zeroes are 0 and -2
Verification:
α= 0 β= -2
α+β= -
, Verified
αβ= constant term/ coefficient of
, verified.
Therefore the zeroes are
Verification:
α= β=
α+β= -
verified.
αβ= constant term/ coefficient of
=
verified.
Therefore the zeroes are
verification:
α= β= -1
α+β= -
, verified
αβ= constant term/ coefficient of
, verified.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:
(i) (ii)
(iii)
(iv) 1, 1 (v)
(vi) 4, 1
(i) Let the required polynomial be ax² + bx + c, and let its zeroes  and
and 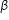
α+β=
αβ =
 and
and 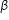
 and
and 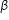
 and
and 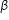
 and
and 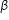
 and
and 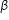
How helpful was it?
How can we Improve it?
Please tell us how it changed your life *
Please enter your feedback
UrbanPro.com helps you to connect with the best Class 10 Tuition in India. Post Your Requirement today and get connected.
Find best tutors for Class 10 Tuition Classes by posting a requirement.

Get started now, by booking a Free Demo Class