We can think of complex numbers as vectors.
Our aim in this section is to write complex numbers in terms of a distance from the origin and a direction (or angle) from the positive horizontal axis.
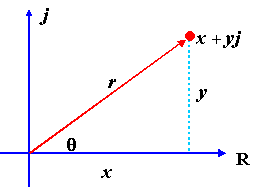
We find the real (horizontal) and imaginary (vertical) components in terms of r (the length of the vector) and θ (the angle made with the real axis):
r2 = x2+y2
tanθ = y/x
x = rcosθ
y = rSinθ
Multiplying the last expression throughout by j(Imaginary number),
yj = jr sinθ
So we can write the polar form of a complex number as:
x+yj = r(cos θ+j sin θ)
r is the absolute value (or modulus) of the complex number
θ is the argument of the complex number.


 0
0

