Application Of Trigonometry

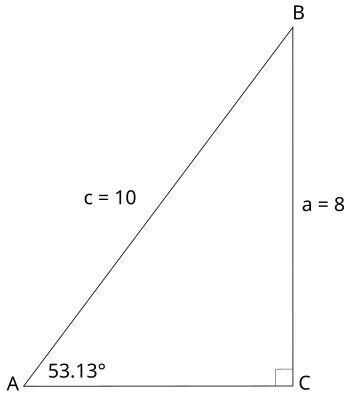
Solve the triangle shown below:

Solution:

We need to find the lengths of all sides and the measures of all angles. In this triangle, two of the three sides are given. We can find the length of the third side using the Pythagorean Theorem:

8 2 + b 2 = {\displaystyle 8^{2}+b^{2}=\,\!}	10 2 {\displaystyle 10^{2}\,\!}
64 + b 2 = {\displaystyle 64+b^{2}=\,\!}	100 {\displaystyle 100\,\!}
b 2 = {\displaystyle b^{2}=\,\!}	36 {\displaystyle 36\,\!}
b = {\displaystyle b=\,\!}	± 6 ⇒ b = 6 {\displaystyle \pm 6\Rightarrow b=6\,\!}

(You may have also recognized the "Pythagorean Triple", 6, 8, 10, instead of carrying out the Pythagorean Theorem.)

You can also find the third side using a trigonometric ratio. Notice that the missing side, b, is adjacent to angle A, and the hypotenuse is given. Therefore we can use the cosine function to find the length of b:

cos ? ( 53.13 ? ) = {\displaystyle \cos(53.13^{\circ })=\,\!}	adjacent side hypotenuse = b 10 {\displaystyle {\frac {\text{adjacent side}}{\text{hypotenuse}}}={\frac {b}{10}}}
0.6 = {\displaystyle 0.6=\,\!}	b 10 {\displaystyle {\frac {b}{10}}}
b = {\displaystyle b=\,\!}	0.6 ( 10 ) = 6 {\displaystyle 0.6(10)=6\,\!}

We could also use the tangent function, as the opposite side was given. It may seem confusing that you can find the missing side in more than one way. The point is, however, not to create confusion, but to show that you must look at what information is missing, and choose a strategy. Overall, when you need to identify one side of the triangle, you can either use the Pythagorean Theorem, or you can use a trig ratio.

To solve the above triangle, we also have to identify the measures of all three angles. Two angles are given: 90 degrees and 53.13 degrees. We can find the third angle using the triangle angle sum:

180 − 90 − 53.13 = 36.87°

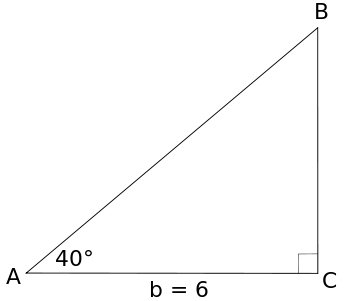
Solve the triangle shown below.

---

Solution: In this triangle, we need to find the lengths of two sides. We can find the length of one side using a trig ratio. Then we can find the length of the third side either using a trig ratio, or the Pythagorean Theorem.

We are given the measure of angle A, and the length of the side adjacent to angle A. If we want to find the length of the hypotenuse, c, we can use the cosine ratio:

cos ? ( 40 ? ) = {\displaystyle \cos(40^{\circ })=\,\!}	adjacent hypotenuse = 6 c {\displaystyle {\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {6}{c}}}
cos ? ( 40 ? ) = {\displaystyle \cos(40^{\circ })=\,\!}	6 c {\displaystyle {\frac {6}{c}}}
c cos ? ( 40 ? ) = {\displaystyle c\cos(40^{\circ })=\,\!}	6 {\displaystyle 6\,\!}
c = {\displaystyle c=\,\!}	6 cos ? ( 40 ? ) ≈ 7.83 {\displaystyle {\frac {6}{\cos(40^{\circ })}}\approx 7.83}

If we want to find the length of the other leg of the triangle, we can use the tangent ratio. (Why is this a better idea than to use the sine?)

tan ? ( 40 ? ) = {\displaystyle \tan(40^{\circ })=\,\!}	opposite adjacent = a 6 {\displaystyle {\frac {\text{opposite}}{\text{adjacent}}}={\frac {a}{6}}}
tan ? ( 40 ? ) = {\displaystyle \tan(40^{\circ })=\,\!}	a c {\displaystyle {\frac {a}{c}}}
a = {\displaystyle a=\,\!}	6 tan ? ( 40 ? ) ≈ 5.03 {\displaystyle 6\tan(40^{\circ })\approx 5.03\,\!}

Now we know the lengths of all three sides of this triangle. In the review questions, you will verify the values of c and a using the Pythagorean Theorem. Here, to finish solving the triangle, we only need to find the measure of angle B:

180 − 90 − 40 = 50°