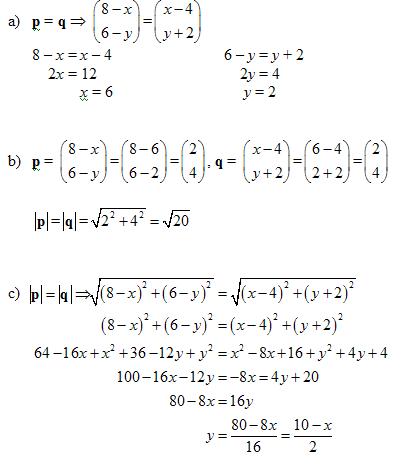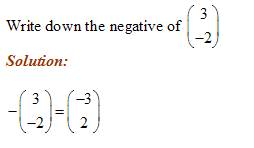0What is Vector?
-
Scalar quantities are quantities that have only magnitudes such as time, area and distance.
-
Vector quantities are quantities that have both magnitudes and directions such velocity (speed and direction), force and acceleration.
-
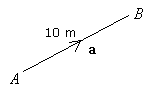
A vector can be represented by a directed line segment, whose direction is given by the arrow and the length shows the magnitude of the vector.
-
The vectors can be denoted by
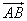or AB or 
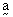or 
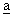or a. -
A is called the initial point and B is called the terminal point of
. -
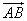The magnitude of a vector is the length of the corresponding segment. The magnitude of
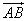is denoted by 
.
-
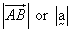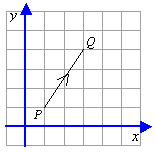
A vector can be written as an ordered pair called a column vector.
-
Consider the line PQ in the diagram. The line represents the translation of P to Q, which is 2 right and 3 up.
-
This can be written as the ordered pair
Example:
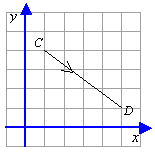
Express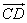 
as a column vector.
Solution:
The translation of C to D is 4 right and 3 down.
Vector Magnitude:
The length of a vector is called the magnitude or modulus of the vector.
Example:
Express each of the following vectors as a column vector and find its magnitude. 
Vectors in 2D:
-
Adding vectors geometrically, scalar multiplication, how to find the magnitude and direction angle of a vector.
-
A vector with initial point at the origin and terminal point at (a, b) is written <a, b>.
-
Geometrically, a vector is a directed line segment, while algebraically it is an ordered pair.
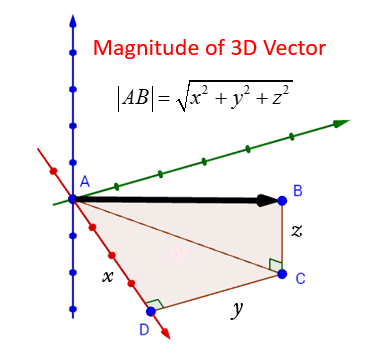
Vectors in 3D
The following diagram shows how to find the magnitude of a 3D Vector.
-
A vector can also be 3-dimensional.
-
The following video gives the formula, and some examples of finding the magnitude, or length, of a 3-dimensional vector.
Equal vectors:
-
Equal vectors are vectors that have the same magnitude and the same direction.
-
Equal vectors may start at different positions. Note that when the vectors are equal, the directed line segments are parallel.
Equality Of Column Vectors:
If two vectors are equal then their vector columns are equal.
Example:
The column vectors p and q are defined by
Given that p = q
a) find the values of x and y
b) find the values of 
and 
c) express y in terms of x
Solution:
Negative Vectors:
The negative sign reverses the direction of the vector.
Example:
Vector Addition:
-
"Nose-to-Tail" Method
-
Vectors can be added using the ‘nose-to-tail’ method or "head-to-tail" method.
-
Two vectors a and b represented by the line segments can be added by joining the ‘tail’ of vector b to the ‘nose’ of vector a. Alternatively, the ‘tail’ of vector a can be joined to the ‘nose’ of vector b.
